During my time as CS student the implementation of a divide and conquer algorithm was pretty straight forward:
- Take an amount of objects (usually an array and usually of type integer)
- Select a pivot element that splits the amount in half
- Do some computation with the two halves. E.g. for sorting make sure that all elements greater than the pivot are contained in one half and the rest in the other.
- Call the algorithm recursively for the two halves.
Since then one thing changed that make it possible to speed the computation up: Multiple CPU cores that allow for multi-threading.
As I was looking for an example of a threaded divide and conquer algorithm, I came up with lots of lectures on the topic but no usable example. It seams this is still an academic topic that has not found its way into the industrial world.
Before we take a peek at the implementation let’s reflect on the problem at hand to see if it is fit for a solution with threads.
- Recursion is effective solution for the memory management. The memory for the amount on which is computed is allocated once.
- The computation is serial, meaning first one half is processed and then the second half
- The 3rd point above ensures that the two halves are autonomous, which means that any manipulation on one half has no effect on the other half.
Especially the third point is good news since it allows an implementation with threads with no inter process communication. That means the thread can be started and the parent can finish as soon as the child is finished but no synchronisation must take place.
The first of the above points is a drawback with threads since the creation and management of threads needs computation time and memory space. Especially with objects more complex than an integer array some data structure must be found that allows efficient computing with threads (Semaphore, mutex, …).
For this article I have chosen the Quicksort algorithm as it is described in Lars Vogel article Quicksort in Java.
One of the first questions to ask is „When is the use of a new thread appropriate for optimizing the computation?“ A rule of thumb says „Create as many threads as you have processors“. Therefore you must now how many processors are present and how many threads you have created. This example focuses on multi-threading on one machine. The results are still valid for a computation in a cluster but there you must consider additional items that concern distributed computing. The following code fragment retrieves the number of processors:
private static int nrOfProcessors;
static {
Runtime runtime = Runtime.getRuntime();
nrOfProcessors = runtime.availableProcessors();
}
Each time a new thread is started the nrOfSpawns is incremented. The variable is initialized with 1 since the current thread must be taken into account. Each time a thread finishes the nrOfSpawns should be decremented.
The tricky part is the recursion. Ensure that the recursion is spawned into a thread when there is an idle processor sitting around. Otherwise compute recursively as in the unthreaded version. In the original the version the integer array is a member of the object. Therefore the array with the boundaries must be passed with the constructor. This works without additional synchronisation only if the above is true.
The complete code with binaries can be downloaded as an eclipse project.
The essential question is: Did we gain something in respect to the computation time. I therefore compared the Array sort from java.util.Arrays with Lars Vogel’s Quicksort and my multi-threaded implementation. The test was executed on a machine with two AMD64 processors on a 32-bit Linux. The X-axis defines the length of the array (0 through 65535 (bigger arrays result in out of memory)). The Y-axis depicts the consumed time in nanoseconds.
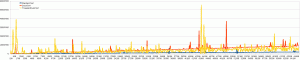
This chart shows two things. Don’t implement a sort algorithm yourself. The one provided by the Java framework is more efficient. The performance of both Quicksort implementations is linear. The threaded implementation performs better especially with large amounts of data. They should perform equally on machines with one processor.